Pore-Space Structure and Fluid Transport in Porous Media

Multiexponential relaxation and “pore size” distribution

  
Comparison between NMR Relaxation time and 
Mercury-Injection pore throat size distributions

  
NMR Estimation of Permeability and Irreducible Water Saturation 

   
Quantitative Relaxation-Tomography applications

POSTERS

Multiexponential relaxation and “pore size” distribution
 

     
Natural rocks, such as sandstones or carbonates, are usually heterogeneous on various distance scales, including scales larger than sizes of the diffusion cells, which may themselves have a wide range of sizes and over which relaxation rates may be averaged. This larger-scale heterogeneity generally leads to multiexponential relaxation, which here is usually inverted by UPEN to obtain the distribution of local S/V ratios, where "local" refers to averages over diffusion cells.
 

visit "Multiexponential relaxation and local diffusion cells distribution" theory HERE

Comparison between NMR Relaxation time 
and Mercury-Injection pore throat size distributions
     
 

NMR measurements respond to local S/V (or V/S, a length) and are usually calibrated so that distributions of relaxations times correspond to distributions of "pore body" dimensions, whereas Mercury Injection (HgI) measures the pore throat and makes the assumption of a simple geometry for the pore volume. Figures show the distributions of pore throat size by HgI (top) and pore body size by relaxation time (bottom) for a sandstone (yellow), a biocalcarenite (blue), and a marble (green). The agreement between shapes of distributions by both methods and relative positions of the peaks is good, despite the different mineral compositions. With a factor of a little over one order of magnitude one goes from the sandstone to the biocalcarenite, and the marble is in the middle for both methods. A difference is the tail at larger times in the sandstone, which could reflect the presence of low S/V pore spaces that are not connected by other low S/V pores, but rather through smaller pores with smaller throats and therefore underestimated by HgI. Each method gives a portion of information; their combination and integration will give a better insight in our knowledge of the pore space.

Although for many materials there is a corrispondence between pore channel sizes measured by mercury injection (HgI) and pore sizes from NMR relaxation, there exist conspicuous exceptions. We observed changes of pore space structure in ceramics sintered at 1280°C for different times. The discrepancy between pore and pore-channel sizes increases dramatically with sintering time and makes it clear that a higher level of sintering allows the formation of larger pores connected by smaller channels. For the samples sintered the longest, scanning electron microscopy and the lack of a NMR signal make it clear tha there is substantial isolates porosity and essentially no connected porosity. [J. Appl. Physics 2003, 5337]
  

NMR Estimation of Permeability 
and Irreducible Water Saturation 
    

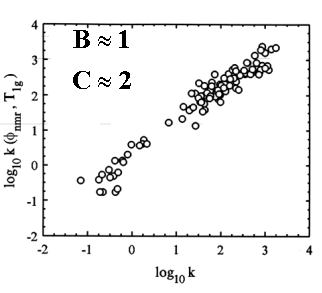
Compact NMR parameters are needed to estimate single parameter, such as permeability k or irreducible water saturation S_wi, of oilfield rocks and other porous media. The strategy of the milestone work of KDSW  (Kenyon, Day, Straley, Willemsen) was to introduce the stretched exponential time, and to look for the best power laws in the form kµf^BT₁^C and proposed kµf⁴T₁². The choice of a form of “average” time can give emphasis to either the larger or else the smaller pores, thus giving the possibility of representing different specific properties of porous media. We used the geometric mean relaxation time, which emphasizes neither short nor long T₁’s [Magn. Reson. Imaging 14: 751-760 (1996)]. On a suite of about 100 sandstone samples we found that by using the geometric mean the best estimator is kµf^0.94T₁^2.23 , with an error factor d=1.8. 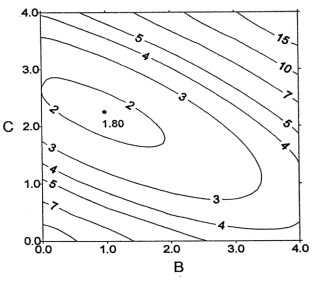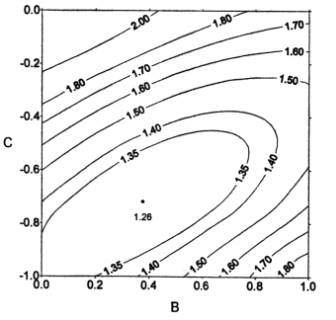The isovalue map (on the right) of the error factor δ as a function of the exponents B and C given to f and T₁ shows that the surface is rather flat in a wide region where δ is not too sensitive to B and C, whereas out of this region the gradients are very high. This can explain why quite different estimators were proposed in the literature, with almost the same error factor.  
That means that porosity and T₁ are not completely independent in sandstones.

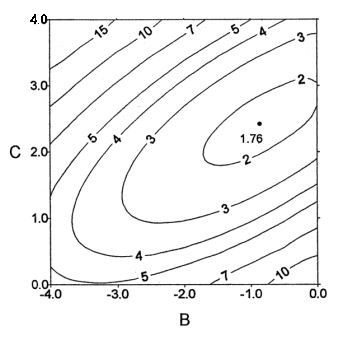
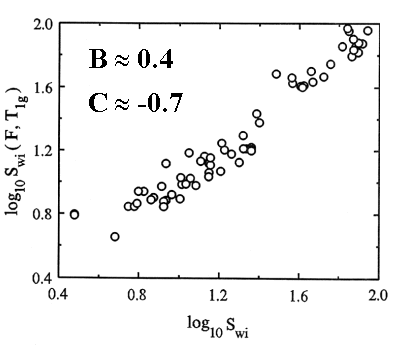
In view of the correlation between f and the electrical-resistivity formation factor F in sandstones (the classical Archie’s law has the form F=f^-m), the same analysis was performed on a subset of 70 samples, for which formation factors F have been measured. The best estimator in the form of a power law was kµF^-0.8T_1g^2.44, with an error factor d=1.76. 
From the isovalue map of the error of the fit (on the right) we get a reasonably good fit of the form: k(F,T₁)µT_1g²/F

      How to overcome the Banavar and Schwartz paradox?


     

   
These relationships clearly show how to overcome the so-called Banavar and Schwartz paradox. At a first glance it would appear that NMR is not a likely candidate to provide information on permeability. In fact, two very similar pore volume geometries, but where the pores are almost blocked or open to the flow, respectively, could have the same relaxation behavior but different permeability properties. Nevertheless, one finds good estimates of k by relaxation times. The explanation presumably consists in some natural regularity existing between pore-node sizes and pore-throat sizes in sandstones. So, it appears evident that the origin of the correlation between k and T₁ or T₂ must be related to their common dependence on the local surface-to-volume ratios in the pore space. The relation with B@1 for f or –1 for F and C@2 for T₁ is consistent with the fact that T₁ has a role of bridge between permeability [L²] and specific surface [L^-1]. F depends on the connectivity of the pore space and, as mentioned, is correlated with f. 
  
  

Estimates also of S_wi have been made with products of powers of f and T or F and T [J. Appl. Physics 75, 1994, 7562-7564; SPE Formation Evaluation 1996, 89-93; Magn. Reson. Imaging 14, 1996, 751-760].
The best estimator on 69 sandstone samples was:    S_wiµF^-0.33T_1g^-0.74 with an error factor d=1.28 or S_wiµF^0.37T_1g^-0.73 with an error factor d=1.2. The analysis of the d isovalue map leads to considerations similar to those for the estimator of permeability.

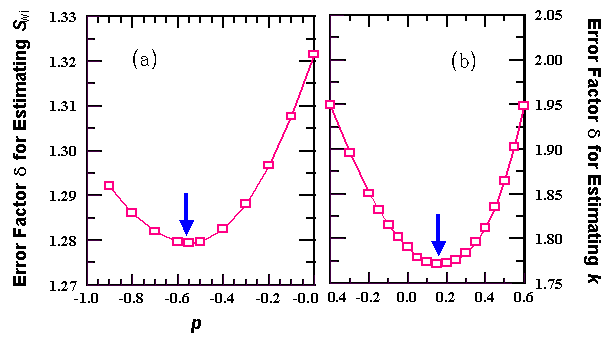
The next step was to get a better insight into the different “average" relaxation times [Magn. Reson. Imaging 14, 1996, 895-897; J. Appl. Physics 82, 1997, 4197-4204; Magn. Reson. Imaging 16, 1998, 625-627; Magn. Reson. Imaging 16, 1998, 613-615]. The choice of a form of average time can give emphasis to longer or shorter times, that is to either the larger or else the smaller pores.  Let us consider  the fractional p-power average  

T^(p)ş<T^p>^1/p

     
For example, T_rms=T⁽²⁾,  T_aa=T⁽¹⁾ , T_ra=T^(-1). This average can give various different emphases to long and short times, depending on the p value, thus giving the possibility of representing different specific properties of the pore space. Given a complex pore system T_ra will give emphases to short times and will be overly influenced by a few small pores (even if T_ra may be appropriate for estimating S/V) [J. Appl. Physics 79, 1996, 3656-3664]. So it is not appropriate for the estimation of k, as  a small volume fraction of very small pores will not greatly decrease fluid flow (unless they are strategically positioned, e.g. in thin impervious laminae, a circumstance which of course does exist in nature). Likewise, T_aa and T_rms will give emphases to long times and will be overly influenced by a few large pores. So these parameters are not the best for correlation with k, since a few larger pores do not contribute much to permeability if they are connected only by small pores and channels. Up to now we used the geometric mean relaxation time. This average time emphasizes neither short nor long T₁’s. 

In fact, T_gm= T⁽⁰⁾=  lim_e®0<T^e>^1/e = exp<lnT>.

The geometric mean is a compromise between mean rate and mean time and does not give undue emphasis to either long or short components.

    
Irreducible water saturation and permeability were estimated by using the fractional p-power average in a suite of water-saturated sandstones. We got a minimum error for the estimation of S_wi at a significantly negative p value (p=-0.55), and we got a minimum error for the estimate of k at a slightly positive p value (p=+0.18). At any given p-value S_wi was fit with a single time parameter (9.44) in the double-exponential form S_wiµ 1-exp[1-exp(9.44/T^-0.55)]. Also for any given p-value, k was fit by varying only the power of T₁, KµfT₁^2.43, where T=T₁^(+0.18).
We concluded that the substantially negative p exponent for estimating irreducible water saturation and the slightly positive p for estimating permeability are compatible with a reasonable picture, where high surface-to-volume pores, giving signal components with short relaxation times but not contributing to the permeability, are important in determining the fraction of the wetting phase which remains trapped in the solid matrix after displacement with a nonwetting phase.

  
Quantitative Relaxation-Tomography applications

A better insight into the structure of a porous medium can be reached by means of Quantitative Relaxation Tomography, allowing one to obtain maps of relaxation times [J. Appl.Physics 90, 2001, 1155-1163; Giornale delle Prove Non Distruttive Monitoraggio Diagnostica XXIII, 2002, 34-40]. The information is very different from that of the proton density images. In fact, in this case the signal in each pixel is proportional to the relaxation time. As an example, a voxel with low relaxation time contains water confined in high S/V ratio spaces, but does not necessarily correspond to a low porosity voxel. In the figure two voxels are represented, having the same porosity, but different pore space structure. The relaxation time of the voxel will distinguish the two structures.
   

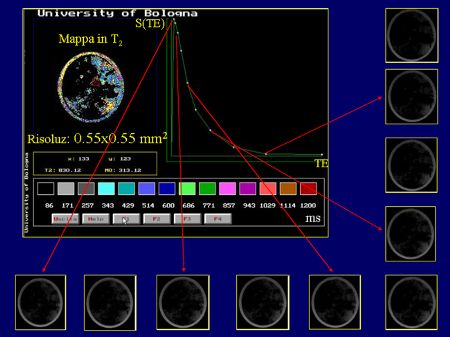
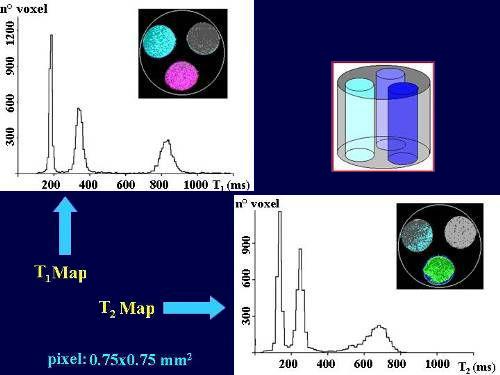
Relaxation time maps are generated by means of suitable pulse sequences and computed by an in-house software written in C++, able to display the maps and the histograms of relaxation times, with many kinds of different weightings, for user-defined regions of investigations (ROI’s).
First of all, SE images were processed.  Voxel by voxel, the signal intensities  obtained at variable TE were fitted to the function

S(TE)=S(0)exp(-TE/T₂)+k,                                        

where k is the offset, to get the extrapolated total equilibrium magnetization S(0)  and the T₂ value.  Then, voxel by voxel, the signal intensities obtained at different  t  values by SR (Saturation-Recovery) sequences at TE=10 ms were fitted, by introducing the corresponding T₂ value of that voxel, to the function

S(t)=S(Ą) [1-k₁exp(-t/T₁)]exp(-TE/T₂)+k₂,               

where k₁ and k₂ are constants, S(Ą) is the total equilibrium magnetization to be compared with S(0), and T₁ is the longitudinal relaxation time to be determined.  The assumptions imply the approximation of single-exponential decay of the transverse and longitudinal components of the ¹H magnetization in each voxel. 

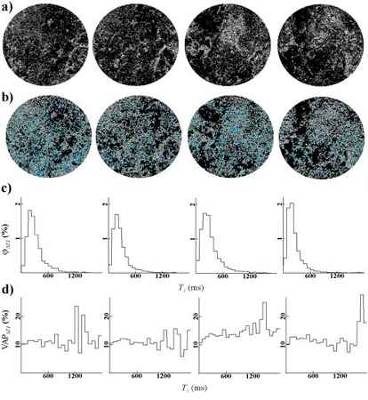
The figure shows maps obtained from a drained Travertine sample from the Roman Theatre of Aosta. After drainage there remained a saturated porosity of (8.8±0.5)%. The images therefore describe only the water contained in the microporosity or in large pores only weakly coupled with each other, representing about three-fourths of the porosity of the sample. Figures a and b show S(0) and T₁ maps, respectively, for four adjacent sections. The signal of each pixel is proportional in S(0) or in T₁ maps to the amount of water or to the relaxation time in the corresponding voxel, respectively. The information encoded in the two kinds of maps is different. A voxel with the same amount of water can have a very different T₁: a low or high T₁ value corresponds to water in high or low S/V regions, respectively. A diffuse microporosity, with regions of lower T₁ and higher S/V, is clearly visible in all sections, connected by a network of channels to regions that are partly emptied if they are connected to the external surface of the sample. Many kinds of histograms can be plotted in order to display different characteristics of the pore space. The histograms in Figure c) represent j_DT1, which in this case constitutes the microporosity distributed as a function of T₁. In this way the area of each column represents the fraction of the total volume of the ROI having that T₁ value, and the total area under the histogram represents the microporosity of the selected ROI. Thus, one finds a marked prevalence of T₁ corresponding to high values of S/V.  Figure d) shows for the same sections the parameter VAP_DT1. This parameter is the Volume-Average-Porosity of the voxels having T₁ in the selected interval. The distributions start at about 10% for low T₁ voxels and tend to increase for higher T₁. That means that the pore-volume averages 10% in voxels with quite high specific surface and about twice as much in voxels with larger pores and relatively low specific surface.